Greetings, my name is Alex Kolar and I’m a rising junior studying Computer Engineering at Northwestern University. This summer, I’ve been working with researchers Rajkumar Kettimuthu and Martin Suchara to develop and implement the Simulator of QUantum Network Communications (SeQUeNCe) to simulate the operation of large-scale quantum networks.
Quantum information networks operate in a similar manner to classical networks, transmitting information and communications between distant entities, but with the added ability to utilize principles of quantum mechanics in data encoding and transmission. These principles include supersposition, by which a single unit of quantum information (qubit) can exist in a probabilistic mixture of different states, and entanglement, by which multiple qubits are affected by actions on one qubit. Many applications are thus available for quantum networks including distribution of secure keys for encryption and reduction of complexity for distributed computing problems.
The simulator, in its current implementation, models the behavior of such networks at the single-photon level with picosecond resolution. This will allow us to test the behavior of complicated networks that cannot be tested without significant time and monetary investment or even within the confines of current optical technology.
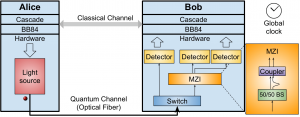
As a test of the simulator, we reproduced the results of an existing physical experiment (see references) to generate secure encryption keys. The simulated optical hardware is shown in Figure 1, where Alice generates the bits for the key and transfers these to Bob.
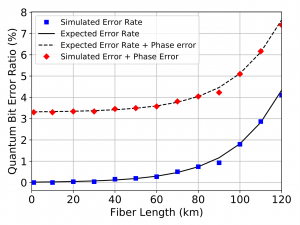
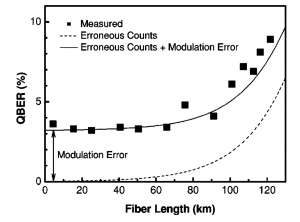
After constructing the keys, we measured the percentage of bits in the keys that differed between Alice and Bob (Figure 2) and compared these to the results of the experiment (Figure 3). Our measured error (blue squares) corresponds closely to the error predicted in the original experiment. We were also able to add a “phase error” to error rate (red diamonds) such that our results matched the experimental results.
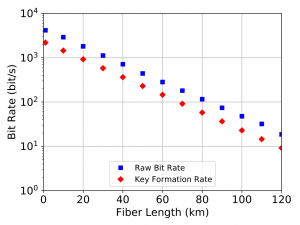
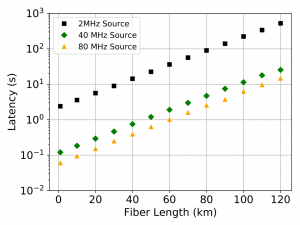
In continuing this simulation, we also were able to generate timing data on the rate of key formation (Figure 4) and latency of key formation (the time until the first key is generated – Figure 5). For the latency, this value was calculated with differing qubit generation frequency, showcasing the ability of the simulator to quickly produce results with varying parameters for its elements.
As shown, SeQUeNCe allows for quick and accurate modeling of quantum communication networks. In the future, this will allow us to test increasingly complicated networks and develop new protocols for their real-world operation.
References:
Month: August 2019
Using Computational Methods as an Alternative to Manual Image Segmentation
Hello! My name is Nicole Camburn and I am a rising senior studying Biomedical Engineering at Northwestern University. This summer I am working with Dr. Marta Garcia Martinez, Computational Scientist at Argonne National Laboratory, with the goal of using machine learning and learning-free methods to perform automatic segmentation of medical images. The ultimate objective is to avoid manually segmenting large datasets (a time consuming and tedious process) in order to perform calculations and generate 3D reconstructions. Furthermore, the ability to automatically segment all of the bone and muscle in the upper arm would allow for targeted rehabilitation therapies to be designed based on structural features.
This past year, I did research with Dr. Wendy Murray at Shirley Ryan AbilityLab, and I was looking at how inter-limb differences in stroke patients compared to healthy patients. Previous work done in Dr. Murray’s laboratory has shown that optimal fascicle length is substantially shorter in the paretic limb of stroke patients [1], so my research focused on whether bone changes occur as well, specifically in the humerus. In order to calculate bone volume and length, it was necessary to manually segment the humerus from sets of patient MRI images. Generally speaking, segmentation is the process of separating an image into a set of regions. When this is done manually, an operator hand draws outlines around every object of interest, one z-slice at a time.
Dr. Murray and her collaborator from North Carolina State University, Dr. Katherine Saul, both study upper limb biomechanics, and some of their previous research has involved using manual segmentations to investigate how muscle volume varies in different age groups. Figure 1 shows what one fully segmented z-slice looks like in relation to the original MRI image, as well as how these segmentations can be used to create a 3D rendering.
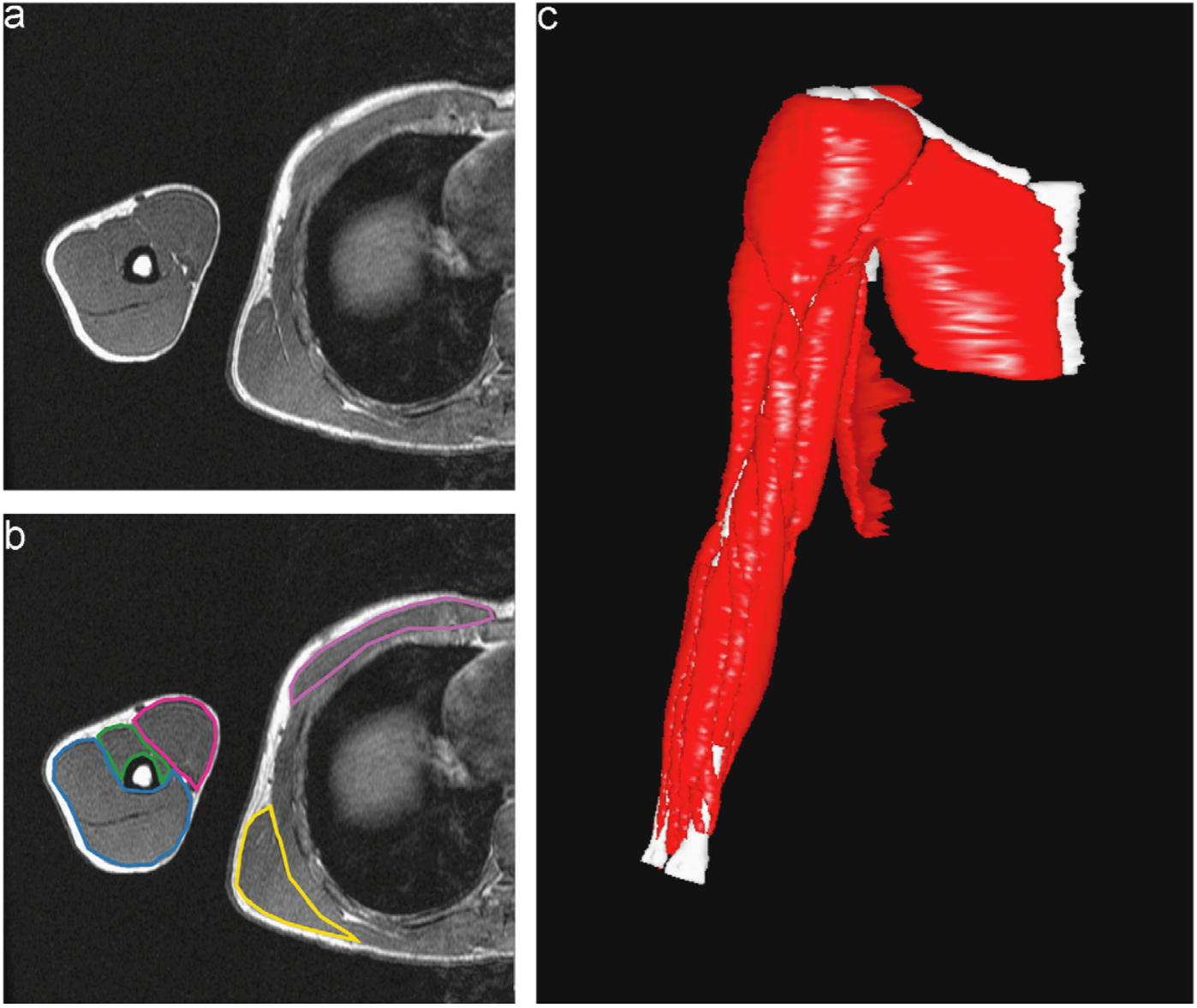
Figure 1: Manually Segmented Features and 3D Reconstruction [2].
In one study, this procedure was done for 32 muscles in 18 different patients [3], and it took around 20 hours for a skilled operator to segment the muscles for one patient. This adds up to nearly 400 hours of manual work for this study alone, supporting the desire to find a more efficient method to perform the segmentation.
For my project so far, I have focused on a single MRI scan for one patient, which can be seen in the following video. This scan contains the patient’s torso as well as a portion of the arm, and 12 muscles were previously manually segmented in their entirety. The humerus was never segmented for this dataset, but because there is higher contrast between the bone and surrounding muscle as compared to between adjacent muscles, it is a good candidate for threshold-based segmenting techniques.
Figure 2: Dataset Video.
One tool I have tested on the MRI images to isolate the humerus is called the Flexible Learning-free Reconstruction of Imaged Neural volumes pipeline, also known as FLoRIN. FLoRIN is an automatic segmentation tool that uses a novel thresholding algorithm called N-Dimensional Neighborhood Thresholding (NDNT) to identify microstructures within grayscale images [4]. It does this by looking at groups of pixels known as neighborhoods, and it makes each pixel either white or black depending on if its intensity is less than or greater than a proportion of the neighborhood average. FLoRIN also uses volumetric context by considering information from the slices surrounding the neighborhood.
FLoRIN’s threshold is set to separate light and dark features, so the humerus must be segmented in two pieces because the hard, outer portion shows up as black on the scan while the inner part appears white. To generate the middle image in Figure 3, I inverted the set of MRI images and fed them through the FLoRIN pipeline, adjusting the threshold until the inner bone was distinct from the rest of the image. Next, I used FLoRIN to separate the three largest connected components, which are the red, blue, and yellow objects in the rightmost image. After sorting the connected components by area, I was able to isolate the inner part of the humerus, which is represented by the yellow component.
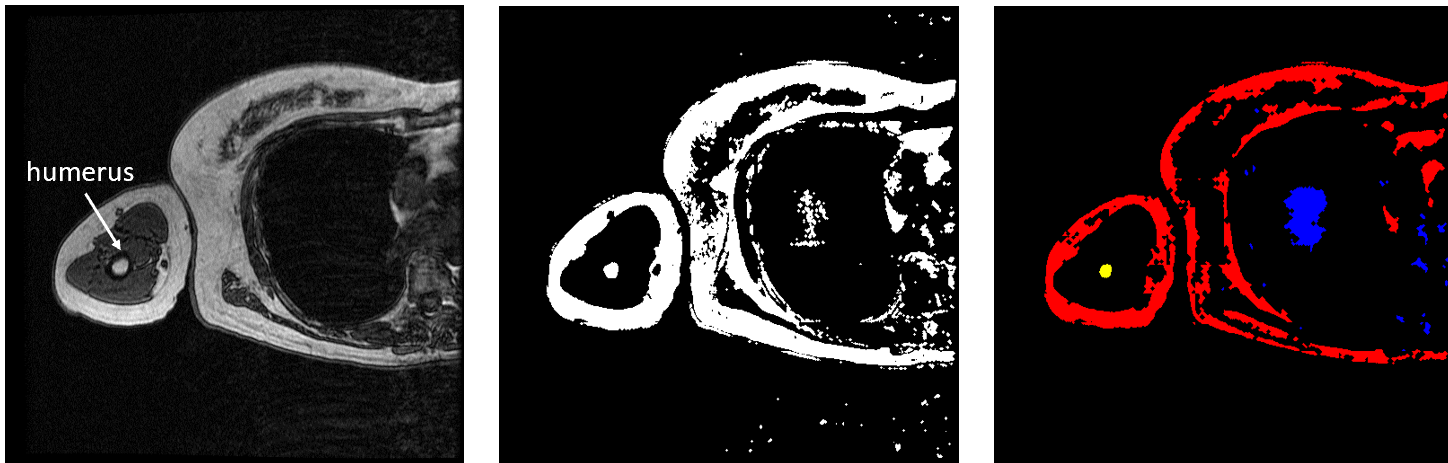 Figure 3: Original Image (left). Light Features as One Object (middle). Three Connected Components (right).
Figure 3: Original Image (left). Light Features as One Object (middle). Three Connected Components (right).
Another method I explored throughout my research was the use of a Convolutional Neural Network (CNN) to perform semantic segmentation, the process of assigning a class label to every pixel in an image. The script used to do this was inherited from Bo Lei of Carnegie Mellon University and was adapted to have additional functionality. To train a CNN to perform semantic segmentation, a set of the original images along with ground truth labels must be provided. A ground truth label is the actual answer in which each object in the image is properly classified, and this process is often done manually. However, because a network can be applied to a larger image set than it was trained on, manually segmenting the labels requires much less time as compared to manually segmenting an entire dataset. The CNN approximates a function that relates an input (the training images) to an output (the labels). The network parameters are initialized with random values and as it is trained, the values are updated to minimize the error. One complete pass through the training data is called an epoch, and at the end of each epoch the model performs validation with another set of images. Validation is the process in which the CNN tests itself to see how well it performs segmentation as it is tuning the parameters. Finally, after training is complete, the model can be tested on a third set of images that it has never seen before to give an unbiased assessment of its performance.
As stated previously, threshold-based techniques cannot be used to segment the individual arm muscles due to the lack of contrast, so I employed machine learning methods instead. For simplicity, I decided to start by training a network to only recognize one muscle class. I chose to begin with the bicep because of all of the upper arm muscles that have been segmented in this scan, it has the most distinct boundaries. This means that the network is being trained to identify two classes total, which are the bicep class and the background class. For this patient, there were 71 images containing the bicep, and I dedicated 59 for training, 10 for validation, and 2 for testing. For each set, I selected images from the MRI stack in approximately equally spaced intervals so that they each contained images that were representative of multiple sections of the bicep. After training a network using the SegNet architecture and the hyperparameters seen in Table 1, I evaluated its performance by segmenting the two full-size test images.
 Table 1: Network Hyperparameters.
Table 1: Network Hyperparameters.
I created overlays of the CNN output segmentations and ground truth labels, and this can be seen below next to the original MRI image for the first test image. The white in the overlay corresponds with correctly identified bicep pixels, the green corresponds with false positive pixels, and the pink corresponds with false negative pixels. The overlay shows that the network mostly oversegmented the bicep, adding pixels where they should not be.
 Figure 4: Test Image 1 (far left). Ground Truth Label (middle left). NN Output (middle right). Overlay (far right).
Figure 4: Test Image 1 (far left). Ground Truth Label (middle left). NN Output (middle right). Overlay (far right).
In addition to assessing the network’s performance visually, I also calculated two metrics, which are the bicep Intersection over Union (IoU) and boundary F1 score. Bicep IoU is calculated by dividing the number of correctly identified bicep pixels in the CNN segmentation by the total bicep pixels present in both the ground truth label and the prediction. Boundary F1 score indicates what percentage of the segmented bicep boundary is within a specified distance (two pixels in our case) of where it is in the ground truth label. This network had a bicep IoU of 64.1%, and average boundary F1 score of 23.8%.
After training a network on the full-size images, I decided to try training on a set of cropped images to see if this would improve segmentation. The theory behind this test was to remove the majority of the torso from the scan because it contains features that have similar grayscale level as the bicep. This was done using a MATLAB script that takes a 250×250 pixel area from the same images used previously to train, validate, and test. This script as well as the one used to create the overlays were both inherited from Dr. Tiberiu Stan of Northwestern University. The coordinates were chosen so that the images could be cropped as much as possible without excluding any bicep pixels, which is portrayed in the set of videos below.
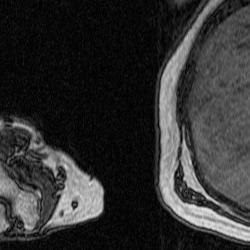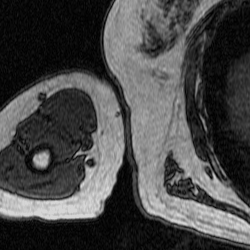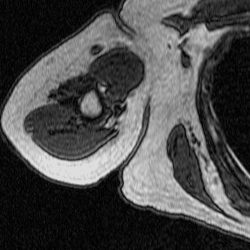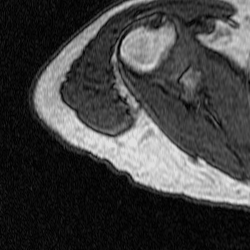

Figure 5: Cropped Images (left) and Labels (right).
When comparing both networks’ bicep segmentations for the two test images, it is apparent that the network trained on cropped images predicted cleaner bicep boundaries. This is especially noticeable in the second test image because the green false positive pixels are in a much more uniform area surrounding the bicep. However, the network trained on cropped images had slightly a lower bicep IoU and boundary F1 score, which were 62.9% and 18.2% respectively. The cropped network also confused a feature in the torso with the bicep, which was not an issue for the network trained on full-size images.
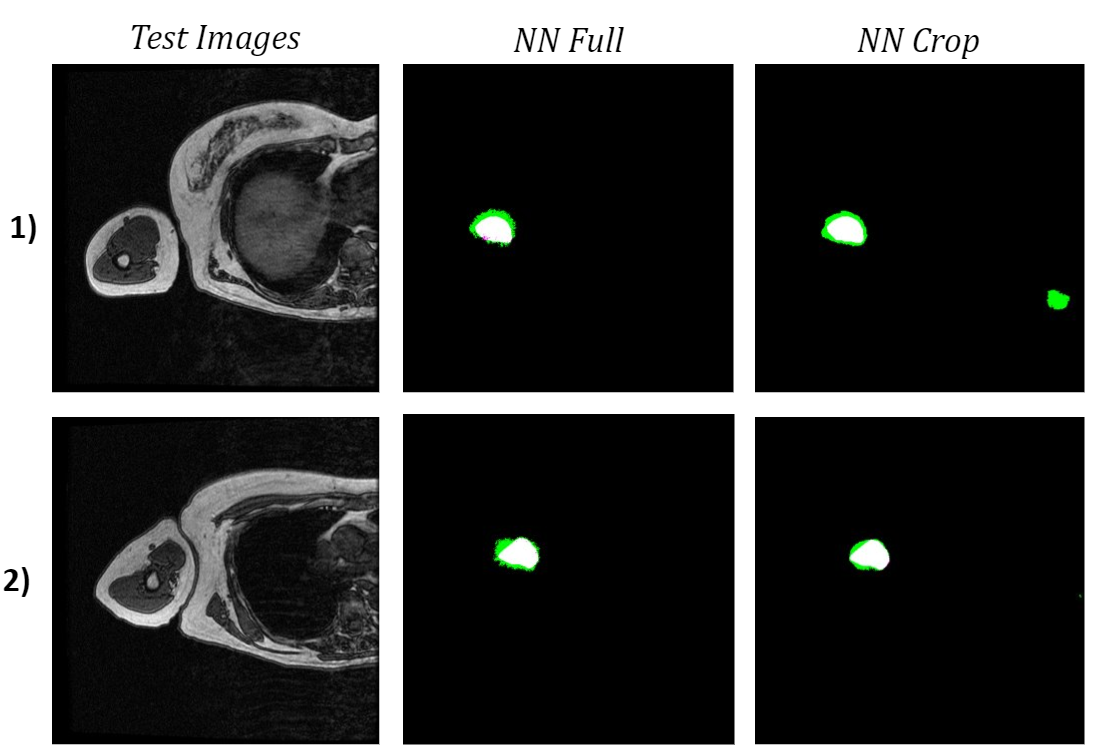
Figure 6: Comparison of Test Image Segmentations.
To see how the networks performed on a more diverse sample of MRI slices, I tested them both on the 10 validation images used in training. The neural network trained on the full-size images once again had a higher bicep IoU and often did a better job of locating the bicep. Although the cropped network typically had cleaner boundaries around the bicep, which is most obvious in the middle two images of the four examples below, it consistently misidentified extraneous features as the bicep.

Figure 7: Comparison of Validation Image Segmentations.
I hypothesize that the network trained on cropped images does this because it never saw those structures during training, so it cannot use location-based context to learn where the bicep is relative to the rest of the scan. Therefore, I anticipate that this actually caused more confusion due to the similar grayscale value of other muscles instead of minimizing it like I had hoped. Despite the current limitations, these results show promise for using machine learning methods to automatically segment upper arm muscles.
Moving forward, my main goals are to generate a cohesive segmentation of both parts of the humerus using FLoRIN as well as improve the accuracy of the bicep neural network. To segment the outer portion of the humerus, I plan to further tune FLoRIN’s thresholding parameters to separate it from the surrounding muscle. Once the segmentations are post-processed to combine the inner and outer parts of the bone, they have the potential to be used as labels for machine learning methods. As for the bicep neural network, I am in the process setting up a training set with multi-class labels that contain two additional upper arm muscle classes, namely the tricep and brachialis. My hope is that having more features as reference will improve the network’s ability to accurately segment the bicep boundary because these are the three largest muscles in the region of the elbow and forearm [2] and often directly border one another. Further improvement in the identification of the anatomical features within the upper arm has great implications for the future of rehabilitation. Knowledge of shape, size, and arrangement of these attributes can provide insight into how different parts are interrelated, and the ability to gather this information automatically has the potential to save countless hours of manual segmentation.
References:
- Adkins AN, Garmirian L, Nelson CM, Dewald JPA, Murray WM. “Early evidence for a decrease in biceps optimal fascicle length based on in vivo muscle architecture measures in individuals with chronic hemiparetic stroke.” Proceedings from the First International Motor Impairment Congress. Coogee, Sydney Australia, November, 2018.
- Holzbaur, Katherine RS, Wendy M. Murray, Garry E. Gold, and Scott L. Delp. “Upper limb muscle volumes in adult subjects.” Journal of biomechanics 40, no. 4 (2007): 742-749.
- Vidt, Meghan E., Melissa Daly, Michael E. Miller, Cralen C. Davis, Anthony P. Marsh, and Katherine R. Saul. “Characterizing upper limb muscle volume and strength in older adults: a comparison with young adults.” Journal of biomechanics 45, no. 2 (2012): 334-341.
- Shahbazi, Ali, Jeffery Kinnison, Rafael Vescovi, Ming Du, Robert Hill, Maximilian Joesch, Marc Takeno et al. “Flexible Learning-Free Segmentation and Reconstruction of Neural Volumes.” Scientific reports 8, no. 1 (2018): 14247.
Digitalize Argonne National Lab
Author: James Shengzhi Jia, Northwestern University, rising sophomore in Industrial Engineering & Management Science
Imagine if you are a researcher here at Argonne, and you don’t have to go upstairs downstairs all the time just to check the experiments that you are running — all you have to do is sit in front of the computer, monitor and control all of them in one system. Wouldn’t that be amazing?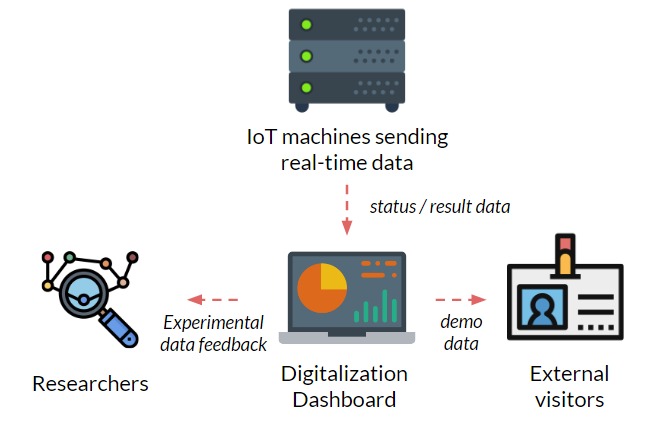
Figure 1: Schematic of the project motivation
Before this internship, I couldn’t possibly imagine such a scenario. However, during the summer, I was working with my mentor Jakob Elias at Energy and Global Security Directorate and creating the beta infrastructure of the system that can connect and visualize real-time data from IoT machines at Argonne, and achieve automatic optimization of experiments.
The following short videos demonstrated the beta infrastructure that I created. It’s easy to navigate through the interactive map, and obtain key information about the areas, buildings, rooms and experiments that are of your interest. The dashboard is able to receive data from the local system, websites and also MQTT protocol. In the future, we plan to integrate various AI applications into the dashboard, so it becomes even smarter and grants researchers full control of their experiments right in their office. 
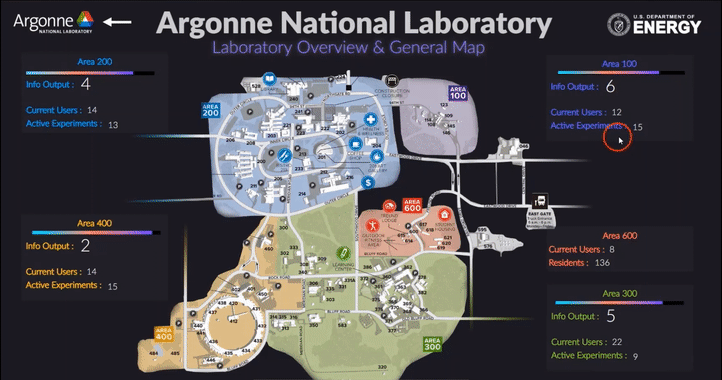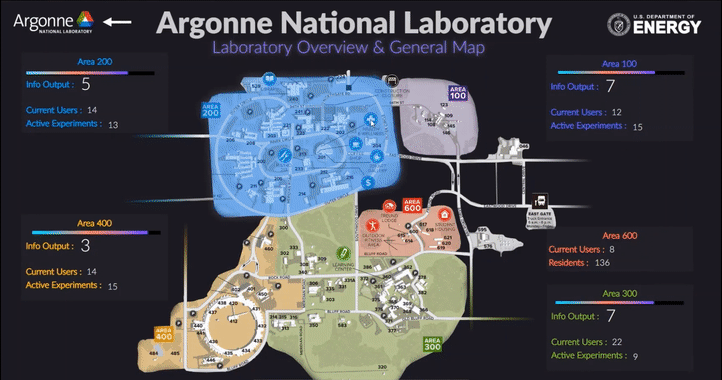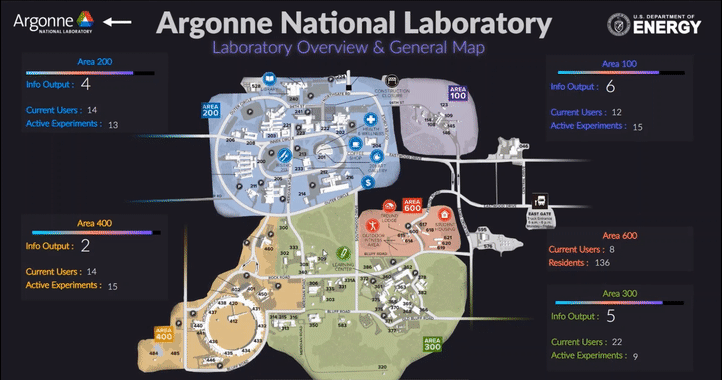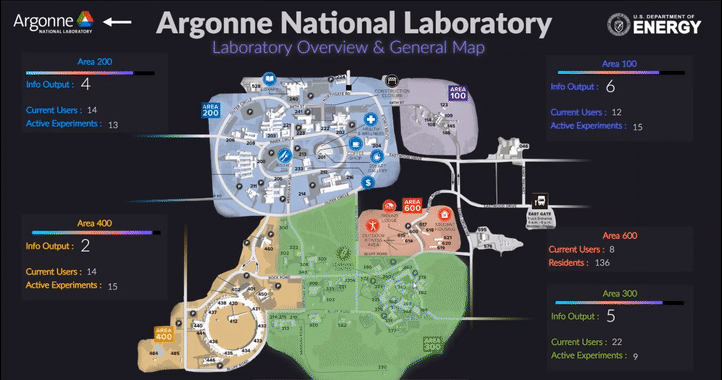


The second part of my work is testing the usability of this dashboard by using the metal 3D printing experiment in Applied Materials Department (AMD) as a test case. Let me give you a brief introduction of the experiment and their objective: (Full explanation can be seen in Erkin Oto’s past post)
AMD researchers at Argonne utilize powerful laser beam, X-ray and IR to conduct metal 3D printing experiments, and the key objective is to characterize and identify the product defects. However, as X-ray machines (which are used to identify defects) are not as ubiquitous as IR machines, researchers at Argonne are exploring whether it’s possible to only use IR data to identify the defects in the products.
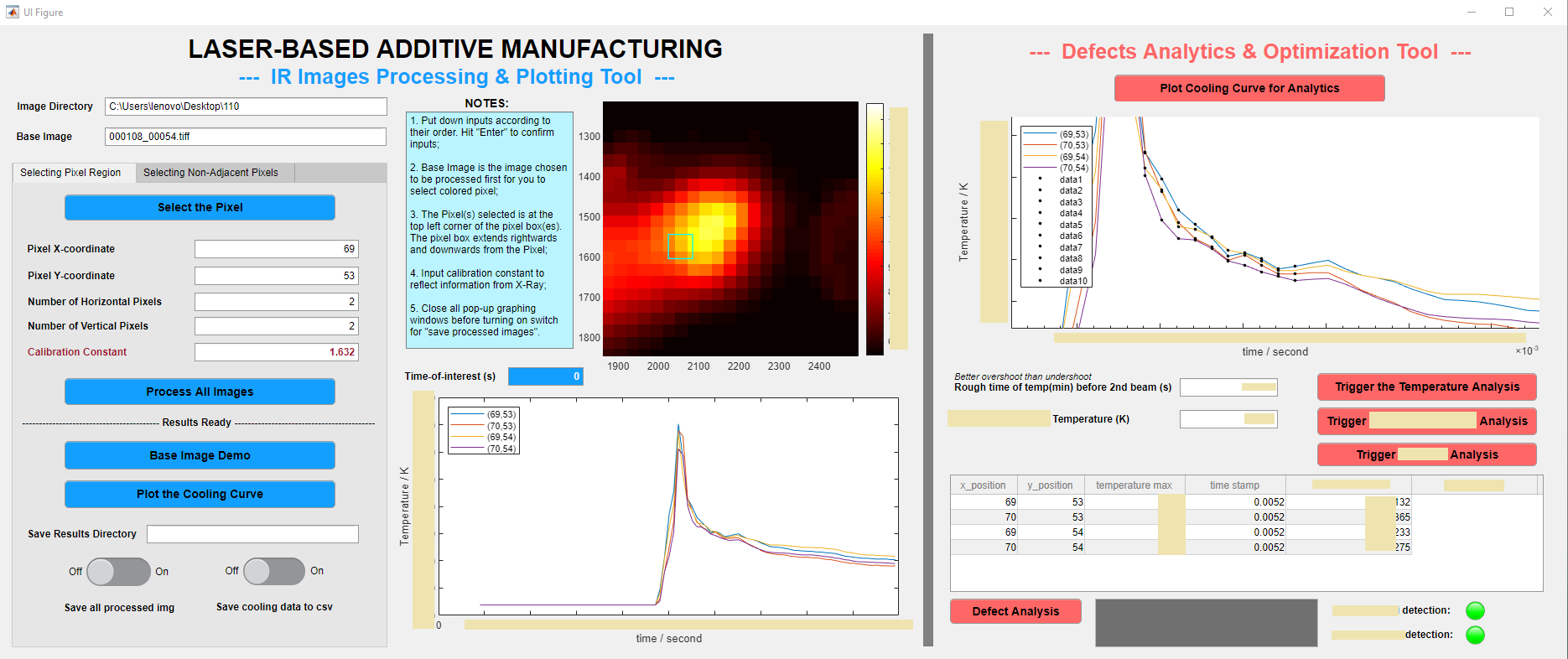
Firstly, as each experiment generates over 1000 IR images, I created a MATLAB software that speeds up the analysis of those images to just within 10 seconds. As shown below, the software works to transform an original black IR image to a fully colored image that researchers can select pixels-of-interest on.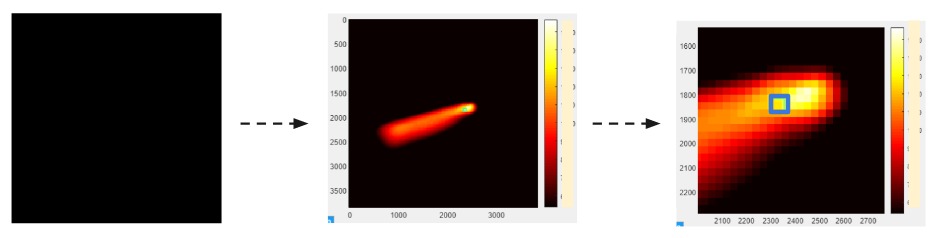
Secondly, additional to the processing tool, I also programmed an analytical tool (which can be seen below) to quantitatively analyze the defect / non-defect dataset. In the process, I came up with two original methods to investigate the correlation, and applied Kernel Gaussian PDF Estimation, Mann-Whitney U Test, and Machine Learning via logistic regression. 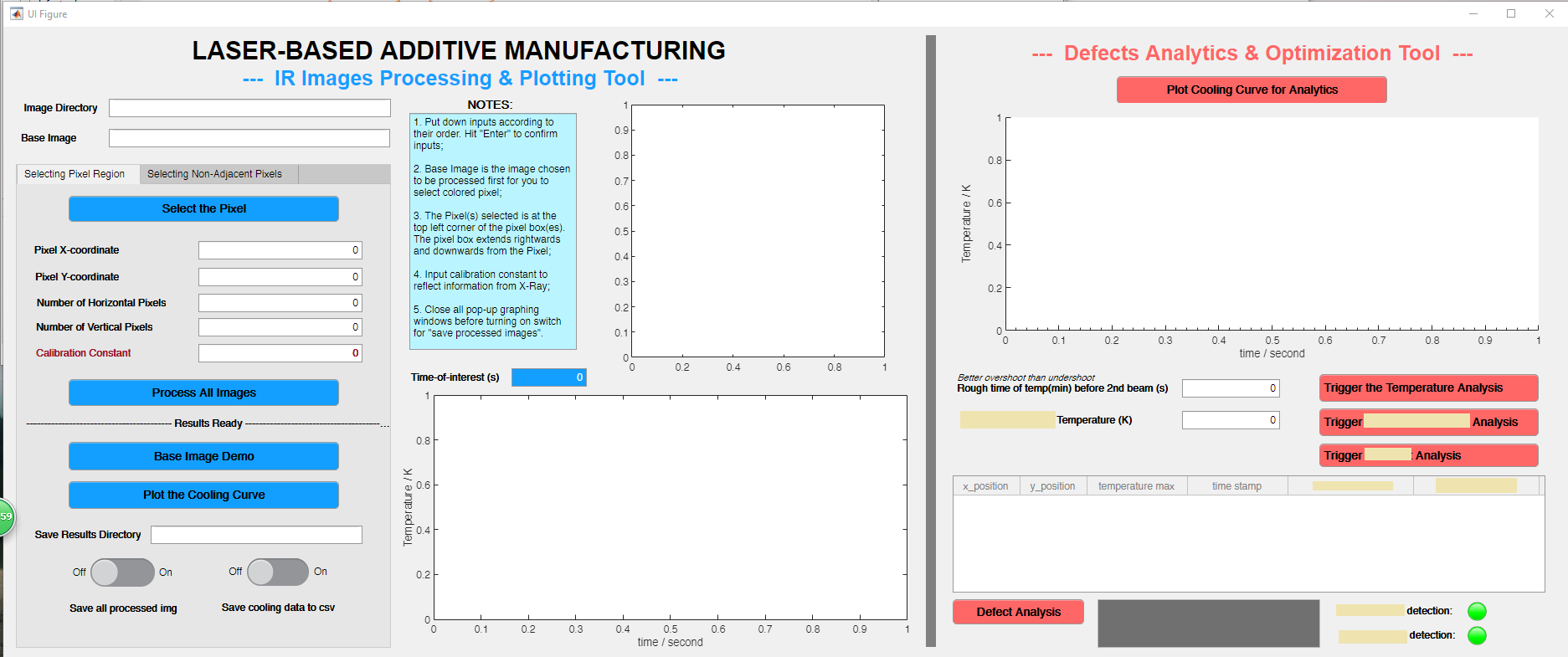
 Based on the original methods that I developed and therefore the machine learning model trained, the accuracy of the model reaches 86.3%, with p values for both method coefficient below 0.1.
Based on the original methods that I developed and therefore the machine learning model trained, the accuracy of the model reaches 86.3%, with p values for both method coefficient below 0.1. 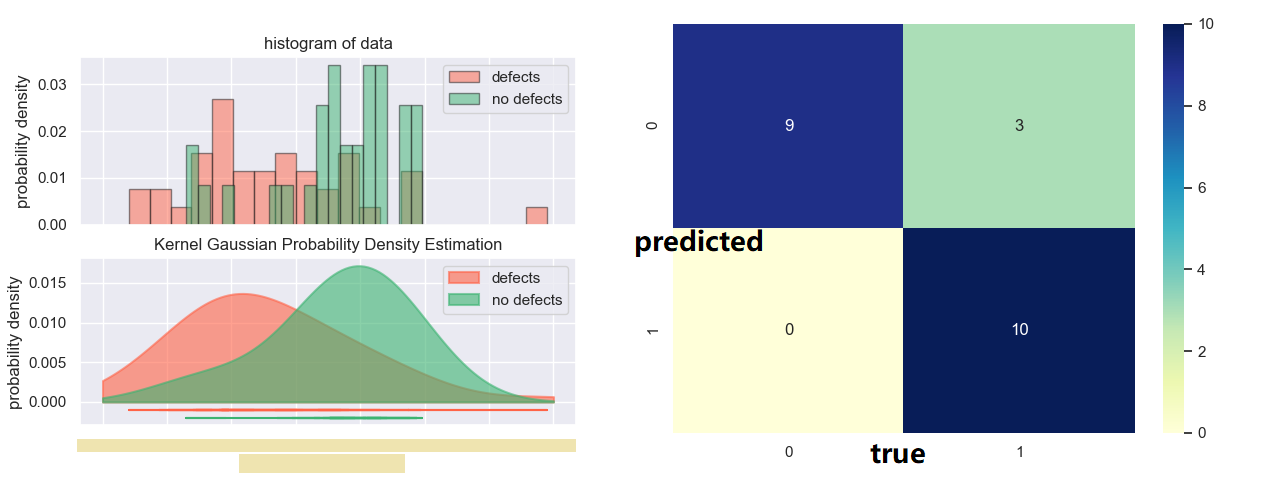
In the future, more efforts can be put into obtaining more accurate data, to improve the model. In a bigger picture, we can also explore about integrating applications like this into the dashboard, and achieve the digitalization of Argonne National Lab in the near future.
Disclaimer: all blocked image data are intended to protect the confidentiality of this project. Unblocked data are either trivial or purely arbitrary (such as ones in prototype dashboard).
Efficiency Optimization of Coherent Down-conversion Process for Visible Light to the Telecomm Range
Hello, my name is Andrew Kindseth and I am a rising junior at Northwestern University. I am majoring in Physics and Integrated Sciences. This summer I am working with Joseph Heremans, a physicist and material’s scientist who is working on the Quantum link and solid state defects that can be used as quantum bits. My project involves making optically addressable solid state defects compatible with existing fiber optic infrastructure. I am also attempting to improve on transmission distances. I expect to accomplish these goals using a process called difference frequency generation.
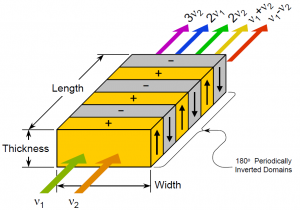
Difference frequency generation (DFG) is a three wave mixing process which takes place in a nonlinear crystal with a high X(2) term. This term refers to the polarization response of the crystal to an electric field. When two waves of frequency w1, w2 pass through the crystal the X(2) term results in the generation of electric waves of 2w1,2w2, w1+w2, and w1-w2. A process called phase-matching can then be used to increase the amount of mixed light received from the process. The technique applied uses a process called quasi-phase matching, which is performed by using a crystale that has opposite orientations of the crystal lattice with specified period. This is called periodically poling. Our crystal is periodically poled with period such that we will generate photons of frequency w1 -w2 when performing our experiment.
By controlling the relative energy densities of each of the respective frequencies of light, the conversion efficiency can be made to rise. This efficiency maximum occurs when one of the light frequencies is much stronger in power then the other. It is the lower power light that is converted efficiently. In the case of single photon pulses on one or either of the input light frequencies the conversion efficiency can become significant, and values of 80% have been demonstrated in experiments.
When one or both of the sources is pulsed the photon emission from the crystal is time correlated with the presence of both frequencies of light in the crystal. If energy imbalance and pulsing are combined, using a single photon pulse on one of the input frequencies, the efficiency and time correlation results in single photon down-conversion.
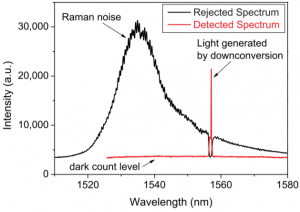
I am working on creating a down-conversion setup here at Argonne for downconversion of light from 637nm to 1536.4nm. The input light to the crystal will then be 637nm light and 1088nm light, with the 1088nm light having a vastly stronger power. The focus of my project is overall efficiency of the process, as well as minimizing the stray photons that may be detected through optical and spatial filtering. For spatial filtering I am using a prism pinhole pair in order to spatially separate the two input wavelengths from the output wavelength of 1536.4nm. This will require painstaking alignment and spectrum analysis. For optical filtering I am using a free space bragg grating. The bragg grating will filter out the Raman and Stokes-Raman noise that is much closer in wavelength to my output wavelength than the input wavelengths.
The relevance of this project arises from the field of quantum information. One of the goals of the field of quantum information is the creation of quantum information networks, as well as transmission of quantum information over large distances. One of the prime candidates as a carrier of quantum information is the photon. Photons are coherent over arbitrarily long distances in free space, and have low transmission loses. However, existing infrastructure for transport of photons only maintain the desirable properties of photons for photons of particular energies. The telecomm band is the region for which fiber optic cable has low transmission loss. For classical computers this frequency range is not problematic because the digital information is transmitted at the desired frequency. However, transmission of quantum information has only be performed with certain quantum bits (qbits). The qbits which are most technologically mature emit photons in the visible range. This is problematic, the emission wavelength of the qbits cannot be changed, and the transmission losses of visible light are prohibitive for the creation of long-distance communication or networks.
One of the most used photon emitting defects is the Nitrogen Vacancy center (NV center). The NV center is a qbit that emits photons of wavelength 637nm. Being able to down-convert the light from an NV center would allow NV centers to be used, with all of their intrinsic benefits, without crippling the ability to form large networks or send information. Initially, I am using a laser to simulate photons being emitted from the NV center, and trying to improve upon the total efficiency realized. Once the efficiency has been optimized with the laser imitator, the laser imitator will be replaced with an NV center.
Connections between nodes in quantum information networks are not the same as for classical networks. One method for forming a connection is to establish entanglement between nodes. This has been done over short distances between two of the same type of qbit. Our overall goal is twofold: to establish entanglement between two different types of qbits, and to do so over a longer distance than has been possible before. I expect that successful and efficient down-conversion will enable this to be acomplished.
Optimizing Neural Network Performance for Image Segmentation
Hi! My name is Joshua Pritz. I’m a rising senior studying physics and math at Northwestern University. This summer, I am working with Dr. Marta Garcia Martinez in the Computational Science Division at Argonne National Lab. Our research concerns the application of Neural Network based approaches to the semantic segmentation of images detailing the feline spinal cord. This, too, is part of a larger effort to accurately map and reconstruct the feline spinal cord with respect to its relevant features – namely, neurons and blood vessels.
Prior to outlining my contribution to this work, it’s worth introducing the terminology used above and, thereafter, illustrating why it fits the motivations of our project. Image segmentation, generally, is the process of identifying an image’s relevant features by distinguishing its regions into different classes. In the case of our cat spine dataset, we are currently concerned with two classes: somas, the bodies of neurons in the spine, and background, everything else. Segmentation can be done by hand. Yet, with over 1800 images collected via x-ray tomography at Argonne’s Advanced Photon Source, this task is all but intractable. Given the homogeneity of features within our images, best exemplified by the similarity of blood vessels and somas (indicated in Figure 1 by a blue and red arrow, respectively), traditional computer segmentation techniques like thresholding and K-means clustering, which excel at identifying objects by contrast, would also falter in differentiating these features.
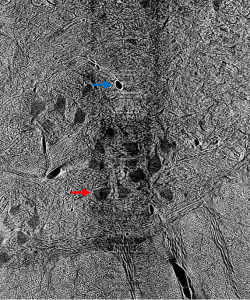
Figure 1: Contrast adjusted image of spinal cord. Blue arrow indicates blood vessel, while red arrow indicates soma.
Enter the Convolutional Neural Network (CNN), through which we perform what is known as semantic segmentation. Herein, a class label is associated with every pixel of an image. A CNN begins by assigning a trainable parameter, a weight, to each pixel in an incoming image. Then, in a step known as a convolution, it performs an affine operation on each submatrix of pixels in the image using a fixed scaling matrix called the kernel, which is then translated using another set of trainable parameters called biases. Convolutions create a rich feature map that can help to identify edges, areas of high contrast, and other features depending on the kernel used. Such operations also reduce the number of trainable parameters in succeeding steps, which is particularly helpful for large input images that necessarily subtend hundreds of thousands of weights and biases. Through activation functions that follow each convolution, the network then decides whether or not objects in the resultant feature map correspond to distinct classes.
This seems like a complicated way to perform an intuitive process, surely, but it begs a number of simple questions. How does the network know whether or not an object is in the class of interest? How can it know what to look for? Neural networks in all applications need to be trained extensively before they can perform to any degree of satisfaction. In the training process, a raw image is passed through the CNN. Its result – a matrix of ones and zeros corresponding respectively to our two classes of interest – is then compared to the image’s ground truth, a segmentation done by hand that depicts the desired output. In this comparison, the network computes a loss function and adjusts its weights and biases to minimize loss throughout training, similar to the procedure of least-squares regression. It takes time, of course, to create these ground truths necessary for training the CNN, but given the relatively small number of images needed for this repeatable process, the manual labor required pales in comparison to that of segmentation entirely by hand.
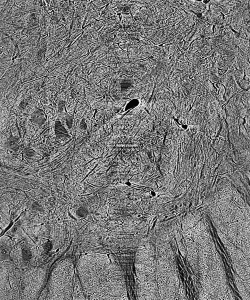

Figure 2: Cat spine image and its ground truth.
The question then becomes, and that which is of primary concern in this research, how can training, and the resulting performance of the CNN, be optimized given a fixed amount of training data? This question lives in a particularly broad parameter-space. First, there are a large number of tunable network criteria, known as hyperparameters (so as not to be confused with the parameters that underlie the action of the CNN), that govern the NN’s performance. Notably, these include epochs, one full pass of the training data through the network; batch-size, the number of images seen before parameters are updated; and learning rate, the relative amount parameters are updated after each training operation. For our network to perform exceptionally, we need to include enough epochs to reach convergence (the best possible training outcome) and tune the learning rate so as to meet it within a reasonable amount of time, while not allowing our network to diverge to a poor result (Bishop).
Second, we can vary the size of images in our training set, as well as the number of them. Smaller images, which are randomly cropped from our full-sized dataset, require a fewer number of trainable weights and biases, thus exhibiting quicker convergence. Yet, such images can neglect the global characteristics of certain classes, resulting in poorer performance on full-sized images. In choosing a number of images for our training set, we need balance whether or not enough data is present to affect meaningful training with oversampling of training data. To conclusively answer our project’s primary question without attempting to address the full breadth of the aforementioned parameter space, we developed the following systematic approach.
Prior to our efforts in optimization, we added notable functionality to our initial NN training script, which was written by Bo Lei of Carnegie Mellon University for the segmentation of materials science images and, herein, adapted to perform on our cat spine dataset. It employs the PyTorch module for open-source accessibility and uses the SegNet CNN architecture, which is noteworthy for its rendering of dense and accurate semantic segmentation outputs (Badrinarayanan, Kendall and Cippola). The first aspect of our adaptation of this script that required attention was its performance on imbalanced datasets. This refers to the dominance of one class, namely background, over a primary class of interest, the somas. To illustrate, an image constituted by 95 percent background and five percent soma could be segmented with 95 percent accuracy, a relatively high metric, by a network that doesn’t identify any somas. The result is a network that performs deceptively well, but yields useless segmentations. To combat this, our additional functionality determines the proportion made up by each class across an entire dataset, and scales the loss criterion corresponding to that class by the inverse of this proportion. Hence, loss corresponding to somas is weighted more highly, creating networks that prioritize their identification.
We also include data augmentation capabilities. At the end of each training epoch, our augmentation function randomly applies a horizontal or vertical flip to each image, as well as random rotations, with fifty percent probability. These transformed images, although derived from the same dataset, activate new weights and biases, thereby increasing the robustness of our training data. Lastly, we added visualization functionality to our script, which plots a number of metrics computed during training with respect to epoch. These metrics most notably include accuracy, the number of pixels segmented correctly divided by the total number of pixels, and the intersection-over-union score for the soma class, the number of correctly segmented soma pixels divided by the sum of those correctly identified with the class’s false positive and negatives (Jordan). We discuss the respective significance of these metrics insofar as evaluating a segmentation below.
Table 1: Hyperparameters used in training.

After including such functionalities our interest turned to optimizing the network’s hyperparameters as well as the computational time needed for training. To address the former, we first trained networks using our most memory-intensive dataset to determine an upper bound on the number of epochs needed to reach convergence in all cases. For the latter, we conducted equivalent training runs on the Cooley and Bebop supercomputing platforms. We found that Bebop offered an approximately two-fold decrease in training time per epoch, and conducted all further training runs on this platform. The remainder of the hyperparameters, with the exception of learning rate, are adapted from Stan et al. who perform semantic segmentation on similar datasets in MATLAB. Our preferred learning rate in this case was determined graphically, whereby we found that a rate of 10-4 did not permit effective learning during training on large images, while a rate of 10-2 led to large, chaotic jumps in our training metrics.
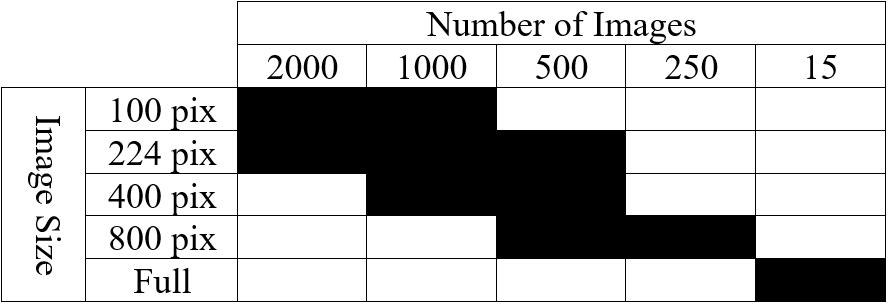
Table 2: List of tested cases depicting image size and number of images in training set.
Using such hyperparameters, listed in Table 1, for all successive training, we finally turned our attention to optimizing our networks’ performance with respect to the size of training images as well as the number of them used. Our initial training images (2300 by 1920 pixels) are very large compared to the size of images typically employed in NN training, which are in the ballpark of 224 by 224 pixels. Likewise, Stan et al. find that, despite training NNs to segment larger images, performance is optimal when using 1000 images of size 224 by 224 pixels. To see if this finding holds for our dataset, we developed ten cases that employ square images (with the exception of full-sized images) whose size and number are highlighted in Table 2. Image size varies from 100 pixels to 800 pixels per side, including training conducted on full-sized images, while image number varies from 250 to 2000. In this phase, one NN was trained and evaluated for each case.

Figure 3: Detail of how smaller images were randomly cropped from full-sized image.
To standardize the evaluation of these networks, we applied each trained NN to two x-ray tomography test images. Compared to the 20+ minutes needed to segment one such image by hand, segmentation of one such 2300 by 1920 pixel image took averagely 12.03 seconds. Resulting from each network, we recorded the global accuracy, soma intersection-over-union (IoU) score, and boundary F-1 score corresponding to each segmentation. Accuracy is often high for datasets whose images are dominated by background, such is the case here, and rarely indicates the strength of performance on a class of interest. Soma IoU, on the other hand, is not sensitive to the imbalance in classes exhibited by our dataset. The boundary F-1 (BF1) score for each image is related to how close the boundary of somas in our NN segmentation is to that of the ground truth. Herein, we use a threshold of 2 pixels, so that if the boundary in our NN’s prediction remains within 2 pixels of the actual soma boundary, the segmentation would receive a 100% BF1 score (Fernandez-Moral, Martins and Wolf). Together with the soma IoU, these metrics provide a far more representative measurement of the efficacy of our network than solely global accuracy. For each network, we exhibit the average of these metrics over both test images in the table below, in addition to heatmaps for soma IoU and BF1 scores.
Figure 4: Heatmaps for BF1 and Soma IoU score for each case.
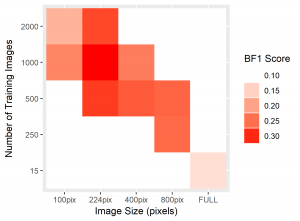
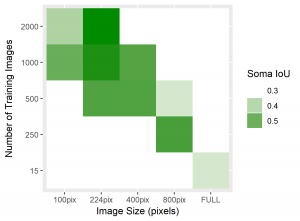

Table 3: Results from test image segmentations.
To visually inspect the quality of our NNs’ output, we overlay the predictions given by each network with the ground truth for the corresponding test image using a MATLAB script developed by Stan et al. This process indicates correctly identified soma pixels (true positives) in white and correctly identified background pixels in black (true negatives). Pink pixels, however, indicate those falsely identified as background (false negatives), while green pixels are misclassified as somas (false positives). We exhibit overlays resulting from a poorly performing network as well as those from our best performing network below.
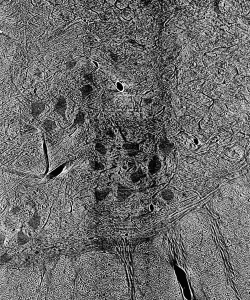

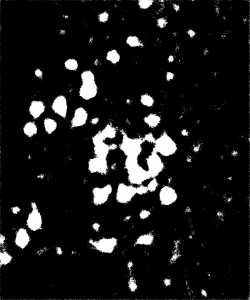
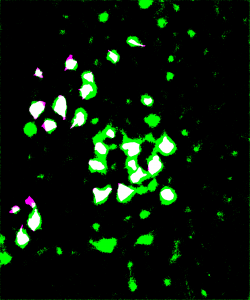
Figure 5: Top: raw test image (left) and test image ground truth (right). Bottom: NN (poorly performing) prediction (left) and overlay of prediction with ground truth (right).
The heatmaps above detailing soma IoU and BF1 scores visually represent trends in network performance with respect to image size and number. We recognize the following. The boundary F-1 score generally decreases when increasing the number of images in the training set. This is most likely due to oversampling in training data, by which resultant networks become too adept in performing on their training data and lose transferability that allows them to adapt to the novel test images. We recognize a similar trend in soma IoU. More so, network performance is seen to appreciate as we decrease the size of training images, until it reaches a maximum in the regime of 224 by 224 pixel images. The decrease in performance of networks trained on larger images may be explained by the lack of unique data. Despite a comparable number of training images, datasets of a larger image size are likely to have sampled the same portion of the original training images multiple times, resulting in redundant and ineffective training. The 100 by 100 pixel training images, on the other hand, are likely too small to capture the global character of somas in a single image given that some such features often approach 100 by 100 pixels in size. Hence, larger images may be needed to capture these essential morphological features. We find that highest performing network is that which was trained using 1000 images of size 224 by 224 pixels, exhibiting a global accuracy of 98.1%, a soma IoU of 68.6%, and a BF1 score of 31.0%. The overlay corresponding to this network shown in Figure 6 depicts few green and pink pixels, indicating an accurate segmentation.



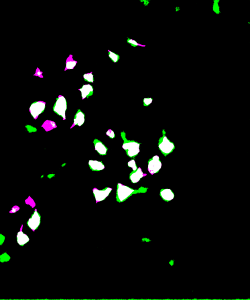
Figure 6: Top: raw test image (left) and test image ground truth (right). Bottom: NN (224pix1000num – best performing) prediction (left) and overlay of prediction with ground truth (right)
Ultimately, this work has shown that convolutional neural networks can be trained to distinguish classes from large and complex images. NN based approaches, too, provide an accurate and far quicker alternative to manual image segmentation and past computer vision techniques, given an appropriately trained network. Our optimization with respect to the size and number of images used for training has confirmed the findings of Stan et al. in showing that networks trained using a larger amount of smaller images perform better than those trained using full-sized images. Namely, our results indicate that 224 by 224 pixel images yield the highest performance with respect to accuracy, IoU, and BF1 scores. In the future, this work may culminate in the application of our best NN to the totality of the feline spinal cord dataset. With appropriate cleaning and parsing of the resultant segmentations, such a network could aid in novel 3D reconstructions of neuronal paths in the feline spinal cord.
References
Badrinarayanan, Vijay, Alex Kendall and Roberto Cipolla. “SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation.” IEEE Transactions on Patter Analysis and Machine Intelligence (2017): 2481-2495. Print.
Bishop, Christopher M. Pattern Recognition and Machine Learning. Cambridge: Springer, 2006. Print.
Fernandez-Moral, Eduardo, et al. “A New Metric for Evaluating Semantic Segmentation: Leveraging Global and Contour Accuracy.” 2018 IEEE Intelligent Vehicles Symposium (IV) (2018): 1051-1056. Print.
Jordan, Jeremy. “Evaluating Image Segmentation Models.” Jeremy Jordan, 18 Dec. 2018, www.jeremyjordan.me/evaluating-image-segmentation-models/. Website.
Stan, Tiberiu, et al. Optimizing Convolutional Neural Networks to Perform Semantic Segmentation on Large Materials Imaging Datasets: X-Ray Tomography and Serial Sectioning. Northwestern University, 19 June 2019. Print.
Optimizing Advanced Photon Source Electrospinning Experimentation
Hi, my name is Jacob Wat and I am a rising junior at Northwestern University. I’m majoring in mechanical engineering with a minor in computer science. This summer, I’ve been working with Erik Dahl, a chemical engineer who is conducting experiments regarding electrospinning and roll to roll manufacturing. As a mechanical engineer, my project deals with the design of a new testing apparatus to increase efficiency and usability.
Electrospinning is a method used to create nanofibers via a polymer solution in syringes, as seen in Figure 1. As the syringe slowly pumps out, a high voltage will draw out the nanofibers to create a deposition on the grounded collector. The collector can change depending on the use; they can be circular or rectangular, flat surface or wires, etc. At Argonne, we use a rectangular, wired collector which is useful for the characterization of nanofibers and one way they are doing that is by taking x-rays of the material at the Advanced Photon Source (APS) to determine different attributes of the material.
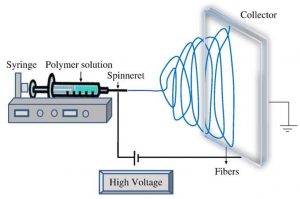
Figure 1. Basic electrospinning setup.
The setup I’m designing for is the APS electrospinning experiments. In Figure 2, you can see that the current implementation has a removable wire collector. It needs to be replaced and the nanomaterial (circled) needs to be cleaned after every iteration. All in all, a very tedious and inefficient method. In order to speed up experimentation, we are designing an apparatus that can run continuously after being initialized in tension.

Figure 2. Picture of wire collector with spun nanofibers present.
With the new electrospinning setup, the most important aspect we were designing for included the continuous lateral movement of the wires, thus allowing users to rotate the spools to a new section of wire remotely. Accordingly, there would be no need to have user oversight; you could start running the experiment, set the motor for the wires to slowly replace the used sections, and leave it to run on its own while continuously collecting data. In addition, many other features had to be redesigned to accommodate this new setup. For example, one of the key parts of electrospinning is the grounding of the collectors (in this case, the wires). To accomplish this, we used grounding bars with notches cut in them to control the spacing between each wire. This solves the problem of grounding and wire spacing with one element of the design. Another important consideration is maintaining tension in the wire. This is achieved via a spring/shock absorber type part that will push against one of the grounding bars so that each wire will always remain in tension. However, each wire has to be individually tensioned before the experiment can begin.
For future development, a prototype should be made and tested at the APS because there are very specific space requirements that have not been dealt with yet. Once it can replace the current implementation, the next step will be to improve the user experience. This could include introducing a method for tensioning all wires at the same time instead of having to do it individually or even go so far as to clean sections of wire to be reused.
References:
Urbanek, Olga. “Electrospinning.” Laboratory of Polymers & Biomaterials, http://polybiolab.ippt.pan.pl/18-few-words-about/17-electrospinning.
Automatic Synthesis Parameter Extraction with Natural Language Processing
Hi there! My name is Peiwen Ren and I am a rising junior studying materials science and integrated science program at Northwestern. This summer, I am working with Jakob Elias and Thien Duong at the Energy and Global Security Institute. My project focuses on using natural language processing (NLP) to automatically extract material synthesis parameters in science literatures.
In recent years, many of the breakthroughs in deep learning and artificial intelligence are in the field of natural language processing. From the speech recognition apps like Siri and Google Assistant, to the question answering search engines, NLP has seen an unprecedented growth of popularity among the AI community. In addition, there have been increasingly more and more applications of NLP in fields like materials science, chemistry, biology and so on. A big challenge in materials science, as well as in chemistry, is that a huge amount of material synthesis knowledge is locked away in literatures. In many cases, after a material is made and the synthesis methods are recorded in a paper, the paper just goes un-noticed. As a result, many potential breakthroughs in materials discovery may have been delayed due to a lack of knowledge of prior work, or unnecessary duplicate studies are conducted only to realize they have been done before. The advantage of NLP, if properly developed, is that it can input a huge amount of texts and output summary information without the need of researchers going through the literatures themselves.
The end goal of this project is to pick out relevant synthesis parameters of the material mentioned in the given abstract or full document text. The advantage of this approach is that if a researcher wants to study a known compound or synthesize a new material, he or she can can just give the name of the compound of interests into the program, and the program will automatically query the existing science literature corpus to download all the papers mentioning the target compound. Then the extracted texts will be fed into a NLP model to pick out relevant synthesis parameter. One example would be given a sentence input, “Compound A was made with compound B by heating in the furnace at 300 degree celsius”, the NLP model would output a tagged sequence with the same length as the input sentence, but each entry corresponds to a pre-defined tag. The tagged output in this case would be “Compound A <TARGET>, was <O>, made <O>, with <O>, compound B <MATERIAL>, by <O>, heating <OPERATION>, in <O>, the furnace <SYNTHESIS-APPARATUS>, at <O>, 300 <NUMBER>, degree <O>, celsius <CONDITION-UNIT>, . <O>” This process of tagging a sequence of word is called named entity recognition (NER).
Here is a list explaining the tags mentioned above:
- <TARGET>: the target material(s) being synthesized
- <O>: null tag or omit tag
- <MATERIAL>: the material(s) used to make the target material(s)
- <OPERATION>: the action performed on material(s)
- <SYNTHESIS-APPARATUS>: equipment used for synthesis
- <NUMBER>: numerical values
- <CONDITION-UNIT>: the unit corresponding to the preceding numerical value
The following figure is a visualization of the tagging.

To realize this NER task, I trained a sequence to sequence (seq2seq) neural network using the pytorch-transformer package from HuggingFace. A seq2seq model basically takes in a sequence and outputs another sequence. The input and output sequence may not be of the same length, although in our sequence tagging task they are. A common use of seq2seq models is language translation, where for example a sequence of English words is put through a model and a sequence of French words is produced, or vice versa.

Since training a seq2seq model is a supervised learning problem (meaning the model needs labeled training set), a hand-annotated dataset containing 235 synthesis recipes was taken from the Github page of Professor Olivetti’s group at MIT. The dataset was downloaded in a nested JSON format, which was then flattened into a csv file using python’s Pandas package. Here is a preview of the training set.
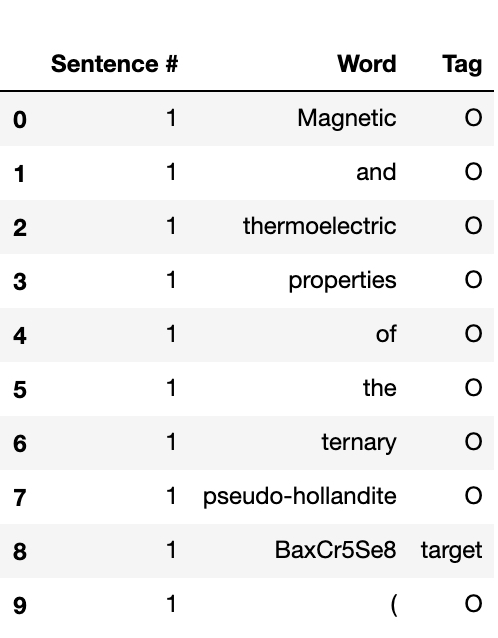
As seen in the figure above, each row represents a word, with “sentence #” specifying the index of the sentence it belongs to and “Tag” representing the pre-defined tag mentioned before. The data was then split into training data and validation/test data in a 90% : 10% ratio. The model was implemented using a pre-trained BERT model from Google Research on a single Nvidia Tesla T4 GPU. After running 5 epochs (1 epoch meaning a passthrough over the entire training set), the prediction accuracy of the model on validation/test set is 73.8%, and the F1 score is 19.8%. A similar model developed by the Olivetti group achieved 86% accuracy and 81% F1 score. [1]
There are two possible reasons for the low accuracy and F1 score:
- The NLP model utilized a NLP model specifically pre-trained on materials science literatures, whereas the BERT was pre-trained on Wikipedia entries and a list of book corpus with little focus on materials science topics.
- The BERT NLP model is predicting a lot of the null tags (“O”) to be meaningful named entities tags. For example, “is” may be predicted as “target” instead of “O”, leading to a large number of false positives in the predicted labels.
The following two figures show a visualization of a sentence prediction from the BERT NLP model.


In the figures above, we can see the the NLP models successfully assign correct tags to most words, except that it misclassifies “magnetic” as a APPARATUS-DESCRIPTOR rather than a SYNTHESIS-APPARATUS, and it fails to assign tags for the last three words “tumbling (60 rpm)”.
The next steps for this project would be to pre-train a model specifically focused on materials science literature and to tune down the false positive rate in the current NLP model, in order to increase the test accuracy and F1 score respectively.
The Jupyter Notebook and training data used for this project will be updated at this Github Repo. The code used for training the BERT model is modified from Tobias Sterbak‘s Named Entity Recognition with BERT post. This project is inspired by the works from Professor Olivetti’s group at MIT and Professor Ceder’s and Dr. Jain’s groups at UCB. [2]
References:
- Kim, E., et al. (2017). “Machine-learned and codified synthesis parameters of oxide materials.” Sci Data 4: 170127.
- L. Weston, V. T., J. Dagdelen, O. Kononova, K. A. Persson, G. Ceder and A. Jain (2019). “Named Entity Recognition and Normalization Applied to Large-Scale Information Extraction from the Materials Science Literature.” Preprint.
3D Printing of Food Waste
Hello, my name is Johnathan Frank, and I am a rising junior studying chemical engineering at Northwestern. This summer, I am researching under Meltem Urgun-Demirtas and Patty Campbell in the Applied Materials Division at Argonne. My work focuses on exploring food waste materials for 3D printing purposes.
The importance of this research is multi-faceted. Plastic usage and waste today constitute a growing problem for the world, as most of the 300 million tons of plastic produced annually are produced from unsustainable petrochemical resources and pose environmental concerns after their use due to many plastics’ inability to biodegrade in receiving environments (natural and engineered). Plastics thus require address to remedy the sustainability issues they create. Food waste disposal is another area that could benefit from new ideas, as current disposal methods are not very economical, but upcycling the annual 1.3 billion tonnes of food waste globally per year would provide a more profitable alternative and help promote a circular economy. Exploring food waste materials as plastic alternatives is a step toward a potential solution to both of these issues.
Previous research in this project focused primarily on investigating alternative food waste options and processing options necessary to form biofilms, and I started this summer as the focus began to more strongly be on 3D printing. Additive manufacturing represents an opportunity for more efficient, sustainable production and so it is an important aspect of the research. Furthermore, the printing setup I use is a home 3D printer that has been modified to allow the cold extrusion of pastes, and the chemicals and raw materials I am using are safe and easy to obtain so there is potential for home printing of similar biocomposites.
This summer, I have largely focused on printing qualities (such as the evenness of print color and texture, strength of the dried prints, and print shrinkage) of chitosan-based biocomposites. Chitosan, derived from chitin that comes from sources such as crustacean shells, fungi, and insect exoskeletons, functions as a binder for the composites, with various powders as fillers. The fillers that I have primarily used are microcrystalline cellulose, carrot, and eggshell, as some representations of food waste that could be used for 3D printing biocomposites. Printing the pastes for these composites presents a couple challenges that I have looked to address.

First, an inherent challenge in using chitosan as the binder is the need to dissolve it in acid. This means that, as the part sets, water evaporates and causes shrinkage of the print, resulting in features losing their integrity and especially posing a risk for complex prints. In tandem with that concern, parts need to be dried evenly and quickly enough while printing to allow extrusion of successive layers onto a stable base. Pastes with high amounts of water tend to shrink a lot, but they are easily printed because they are thinner. For thicker pastes, however, the extruder has more difficulty pumping the paste through the tubing of the printer and could jam. I worked with a number of ratios of chitosan, filler powder, and acid to try to find an optimum paste composition.


Second, the printer and its default settings are not optimized for printing pastes, and even the extruder used that gives the printer the ability to print paste materials is optimized for silicone, not the biocomposite pastes I am using. Pastes with an uneven consistency or sticky texture plug up the extruder or clump on the printer nozzle (unlike silicone, which is homogenous and slippery), and print speed, infill density, and material flow are all tailored by trial and error to produce good print quality. Airflow in the printer is another parameter that has proven to be very important because it allows the partial drying of a part while it is printing to ensure that each successive layer is deposited onto a solid base. Bubbles in the paste as a result of filling the extruder syringe pose two difficulties: the bubbles create gaps in the print surface when they are ‘extruded’ instead of paste, and as bubbles leave the tubing they decrease pressure in the syringe, necessitating a gradual increase in applied pressure in the extruder over time.


As this project develops, it will be necessary to address more aspects of 3D printing these biocomposites, and further fine-tune compositions and parameters to produce consistently successful prints. Also, the mechanical properties and biodegradability of the dried prints will need to be tested. Eventually, this research could open possibilities for more environmentally friendly plastic alternatives and profitable waste disposal, as well as bring us toward a more sustainable circular economy. I would like to thank Meltem Urgun-Demirtas for mentoring me this summer, as well as Dr. Jennifer Dunn and those involved with NAISE for giving me the opportunity to research at Argonne over the summer.
Electrospinning of PVDF/HFP for Paper Conservation Applications
Hello! My name is Kathleen Dewan and I am a rising junior at Northwestern studying materials science and engineering. This summer, I am working with Yuepeng Zhang, whose group specializes in the synthesis of nanofibers using electrospinning. In my project, I am aiming to use electrospinning for the conservation of paper artifacts.
The preservation of cultural heritage is vital to the perpetuation of unique identities and communities within society, as it serves to maintain the histories and records of these cultures for many generations into the future. Paper is one of the oldest substrates used by man for record-keeping, as it was first invented in China around 100 B.C., and a great number of historically pertinent documents are paper-based. There is currently a great emphasis placed on the preservation of these artifacts from chemical degradation, as cellulose-based paper is subject to acidification and oxidation over extended periods of time. However, there are far fewer techniques that exist to protect paper from mechanical wear, which can include tearing, water damage, degradation from UV radiation, and exposure to contaminants.
In order to protect paper artifacts from this kind of damage, the ideal conservation mechanism would be clear, tensily strong, hydrophobic, UV resistant, and able to provide a barrier against common airborne particulates. Due to these requirements, we looked towards electrospinning a blend of polyvinylidene fluoride with hexafluoropropylene (PVDF/HFP) to deposit a near-invisible membrane of nanofibers directly onto a paper substrate. The electrospinning process produces nanofibers by using a voltage source to draw a solution of opposite charge onto it, and this results in the formation of a nanofiber mesh. This mesh structure is ideal for our applications, as it provides a barrier against potential contaminants while still remaining porous enough to maintain the ambient atmospheric conditions that are required for the paper to remain chemically stable. We chose PVDF/HFP for our solution because it is colorless, meaning that the legibility of the paper can be maintained, as well as highly hydrophobic and UV resistant, meaning that it can serve to protect the paper from water and UV damage.
Below is an image of the experimental setup used for electrospinning.

Figure 1: Electrospinning experimental setup
The first step in creating an appropriate membrane is to optimize the morphology of the fibers produced by electrospinning. Because electrospinning is a process that involves many parameters, including spinning time, voltage, injection rate of solution, and concentration of solution, this required the controlling and variation of many variables in order to get the desired results. Overall, the trends that I observed are that higher spinning times resulted in thicker membranes, higher voltages resulted in better overall coverage, and higher injection rates resulted in a greater amount of fibers. For our applications, we needed our fibers to be numerous and provide adequate coverage, while having the membrane still thin enough as to not alter the legibility of the document. It was sometimes challenging to alter the parameters appropriately to achieve these desired results, which I will discuss further below.
We first deposited the fibers onto aluminum foil, in order to provide a initial estimate of the required parameters. We then deposited the fibers onto a paper substrate, in which we found that certain adjustments needed to be made in order to account for the reduced conductivity of the paper and to maintain the legibility of the text. From these experiments we found that the ideal spinning time would be around 3 minutes, as this would allow the fibers to be just visible enough to identify an appropriate area to take an SEM sample, while still thin enough to preserve the legibility of the text.



Figures 2, 3, and 4: Visual determinations of membrane thickness
We then performed analyses of the fibers using SEM imaging in order to examine their microstructures. SEM imaging is necessary to observe the actual morphology of the fibers, as even if the membrane seems thin enough from the naked eye, we need to ensure that they provide even coverage of the substrate. Below are some examples of how altering certain parameters can change the morphology of the fibers.
The sample below was spun on an aluminum substrate at a voltage of 16 kV and an injection rate of 0.2 mL/hr, with varying spinning times. These images showed us that the injection rate of 0.2 mL/hr was too low, as their coverage is not sufficient, even at 3 minutes.

Figure 5: SEM analysis of samples with varying spinning times
The sample below was spun on a paper substrate for 3 minutes at 0.5 mL/hr, with varying voltages. After increasing the injection rate to 0.5 mL/hr, we began to see more effective coverage at 16 kV and 20 kV, but there are still beads of solution that are present on the fibers. This resulted from instability during the electrospinning process, which was likely caused by the solution concentration, and thus viscosity, being too low, as well as the decrease in the conductivity of the voltage source introduced by the paper substrate [1].

Figure 6: SEM analysis of samples with varying voltages
The most recent experiment that I performed used the same spinning time, voltage, and injection rate conditions, but this time with double the concentration of PVDF/HFP in the solution. Because we increased the solution concentration, we hypothesize that the bead formation will decrease due to the increase of the solution viscosity. However, further SEM imaging is still necessary to determine if these conditions will be optimal.
After the fibers have been sufficiently optimized, I can perform an ImageJ analysis of the SEM images in order to determine the sizes of the spaces in between the fibers in the mesh. I can then compare this information to the average diameters of typical airborne contaminants, which can be found in the table below [2]. This will allow me to make a qualitative estimate of whether or not the membranes will be effective in protecting the paper from these contaminants.
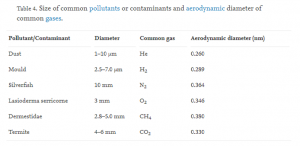
Table 1: Size of common pollutants or contaminants and aerodynamic diameter of common gases.
In the coming weeks, I would also like to performed certain tests on both paper with and without the PVDF/HFP membranes. I would first like to perform tensile tests in order to compare the tensile strength and elongation of each sample, as well as contact angle tests in order to compare the hydrophobicity of each sample. If I still have enough time, I can also perform porosity testing on the paper sample with the membrane in order to determine what kinds of gases the membrane will allow to pass through; this information, in conjunction with Table 1, will help me to determine if the appropriate ambient atmospheric conditions can be maintained with the membrane.
References
1: H Fong, I Chun, D.H Reneker, Beaded nanofibers formed during electrospinning, Polymer, Volume 40, Issue 16, 1999, Pages 4585-4592, ISSN 0032-3861, https://doi.org/10.1016/S0032-3861(99)00068-3.
2: Qinglian Li, Sancai Xi, Xiwen Zhang, Conservation of paper relics by electrospun PVDF fiber membranes, Journal of Cultural Heritage, Volume 15, Issue 4, 2014, Pages 359-364, ISSN 1296-2074, https://doi.org/10.1016/j.culher.2013.09.003.